Equações Diferenciais e RMarkdown

May 19, 2017

Este trabalho tem como objetivo a aplicação de comandos para o RMarkdown. Assim, vamos resolver algumas equações diferenciais ordinárias utilizando o R. As referências utilizadas aqui são [1] e [2]

Modelo de Lorenz

Vamos considerar o modelo de Lorenz, que é um sistema de equações diferenciais dado por

\begin{equation} \begin{split} &\frac{dx}{dt} = ax + yz, \\ &\frac{dy}{dy} = b(y-z), \\ &\frac{dz}{dt} = cy - xy - z. \end{split} \end{equation}

Segue abaixo a solução da equação diferencial acima para os parâmetros

\begin{equation*} a=-\frac{8}{3}, \quad b = -10, \quad c = 28 \end{equation*} 
  library(deSolve)
  a <- -8/3 ; b <- -10 ; c <- 28
  yini <- c(X = 1, Y = 1, Z = 1)
  Lorenz <- function (t, y, parms) {
    with(as.list(y), {
      dX <- a*X + Y*Z
      dY <- b*(Y-Z)
      dZ <- -X*Y + c*Y - Z
      list(c(dX,dY,dZ))
    })
  }
  times <- seq(from=0, to=100, by=0.01)
  out   <- ode(y = yini, times = times, func = Lorenz, parms = NULL)

Após a modelagem da equação diferencial acima, vamos plotar a solução.

  plot(out[,"Y"], out[,"X"], type = "l", xlab = "Y",
       ylab = "X", main = "Solução Borboleta", col="blue")

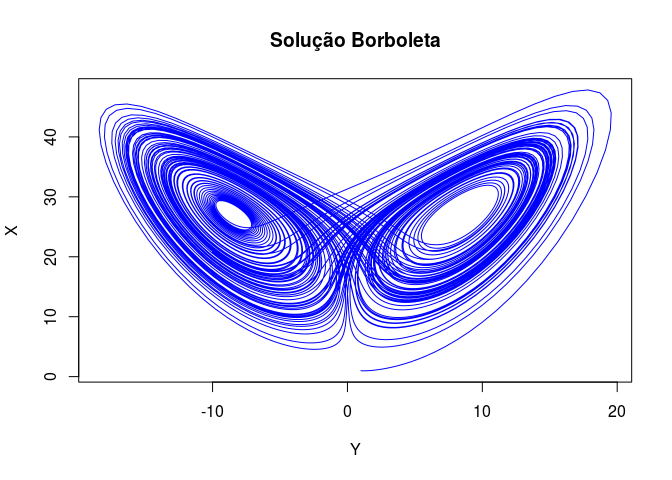
O modelo de Lorenz também é conhecido como Atrator de Lorenz, devido ao comportamento das soluções. Vamos plotar mais algumas soluções para a, b e c distintos.

  a <- -10 ; b <- -8/3 ; c <- 21
  Lorenz <- function (t, y, parms) {
    with(as.list(y), {
      dX <- a*X + Y*Z
      dY <- b*(Y-Z)
      dZ <- -X*Y + c*Y - Z
      list(c(dX,dY,dZ))
    })
  }
  times <- seq(from=0, to=1000, by=0.01)
  out   <- ode(y = yini, times = times, func = Lorenz, parms = NULL)

Sendo o seu gráfico dado abaixo.

  plot(out[,"X"], out[,"Z"], type = "l", xlab = "X",
       ylab = "Z", main = "Solução Fibonacci", col="red")

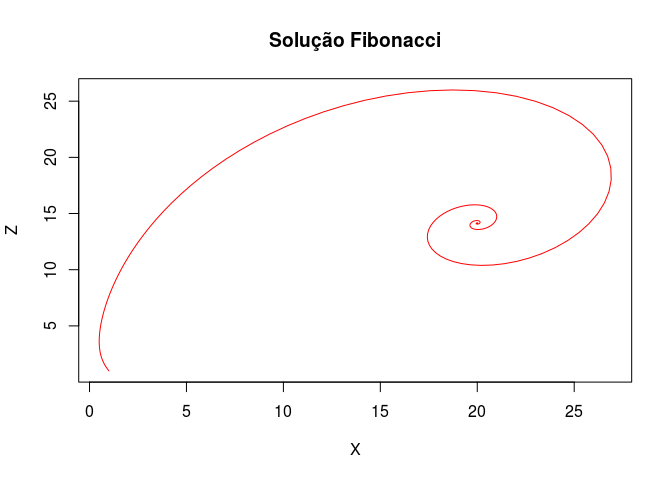
E para outros parâmetros a, b e c, temos que

  a <- -1 ; b <- -8/3 ; c <- 20
  Lorenz <- function (t, y, parms) {
    with(as.list(y), {
      dX <- a*X + Y*Z
      dY <- b*(Y-Z)
      dZ <- -X*Y + c*Y - Z
      list(c(dX,dY,dZ))
    })
  }
  times <- seq(from=0, to=100, by=0.01)
  out   <- ode(y = yini, times = times, func = Lorenz, parms = NULL)

  plot(out[,"X"], out[,"Y"], type = "l", xlab = "X",
       ylab = "Y", main = "Solução Redemoinho", col="cyan4")

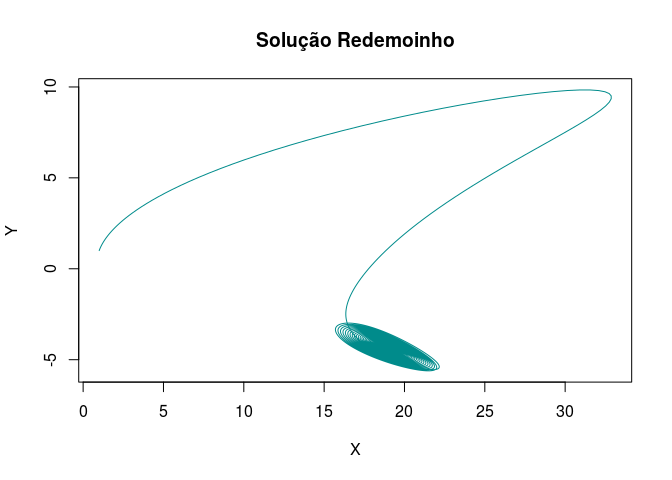
Vamos agora gerar um gif para o último atrator de Lorenz.

  frames = 20
  for(i in 1:frames){
    a <- -1 ; b <- -8/3 ; c <- 20
    Lorenz <- function (t, y, parms) {
      with(as.list(y), {
        dX <- a*X + Y*Z
        dY <- b*(Y-Z)
        dZ <- -X*Y + c*Y - Z
        list(c(dX,dY,dZ))
      })
    }
    times <- seq(from=0, to=i, by=0.01)
    out   <- ode(y = yini, times = times, func = Lorenz, parms = NULL)
    name = paste('0',i,"plot.png",sep='')
    png(name)
    plot(out[,"X"], out[,"Y"], type = "l", xlab = "X",
         ylab = "Y", main = "Solução Redemoinho", col="cyan4")
    dev.off()
  }

Acima geramos as imagens para criar um gif. Para juntar as imagens, temos que usar o terminal. Para tanto, basta entrar no diretório onde as imagens estão salvas e rodar o seguinte código

convert *.png -delay 3 -loop 10000000 redomoinho.gif

Assim, temos o seguinte gif.

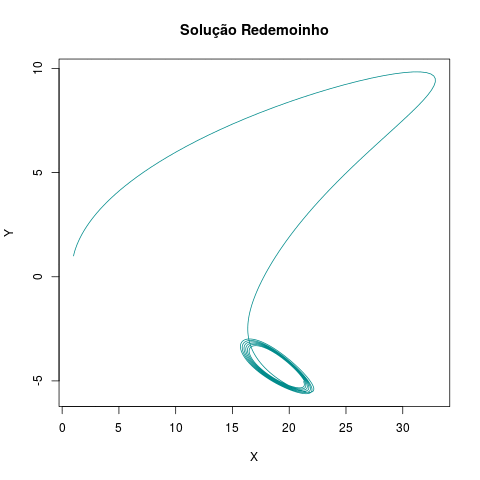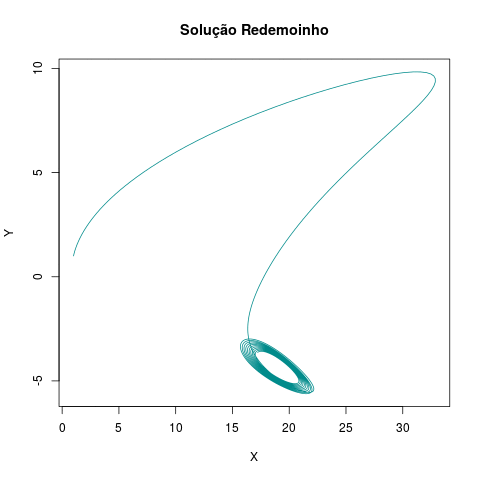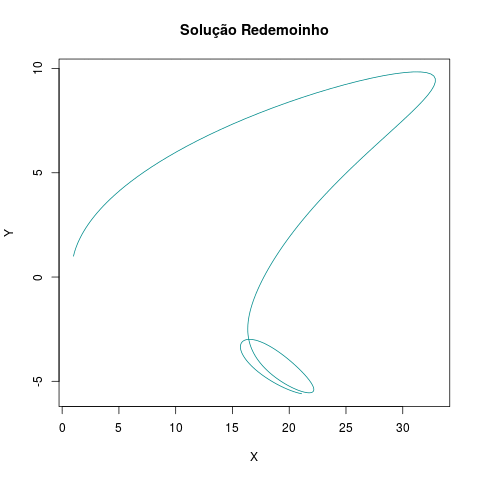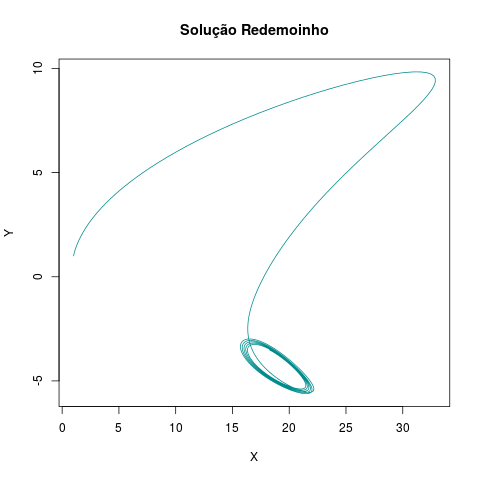
Com isso, encerramos a primeira Atividade do curso de RMarkdown.

Equações Diferenciais e RMarkdown - May 19, 2017 - carlos ronchi